PVITELLI.NET - Le pile di Gergonne

Uno dei primi giochi "matemagici" di carte che ho imparato, era quello che all'epoca chiamavo "gioco delle 21 carte".
Non ricordo con precisione la fonte, ma mi pare fosse un piccolo manualetto di magia divulgativa scritto dal mago Silvan. Il gioco, con tutte le sue varianti, è noto in letteratura con il nome di "Pile di Gergonne" (dal nome del matematico Joseph Diaz Gergonne che per primo se ne occupò).

Il gioco delle 21 carte

Per il gioco, come già detto, si utilizzano 21 carte.
Si distribuiscono tali carte orizzontalmente, una riga alla volta, a formare 3 file di 7 carte ciascuna.
Dopo di che si fa scegliere una carta allo spettatore, e ci si fa comunicare la fila in cui essa si trova.
A questo punto si chiudono le file e si riuniscono i 3 mazzetti, avendo cura di porre nel mezzo il mazzetto contenente la carta scelta dallo spettatore.
Ciò fatto, si ripete l'operazione per altre 2 volte.
Al termine, dopo l'ultima ricomposizione del mazzo, l'undicesima carta a partire dalla cima sarà quella scelta dallo spettatore.
Questo in breve il gioco. Spiegazioni più dettagliate del funzionamento si possono trovare facilmente in rete.

Illustrazione del 'Gioco delle 21 carte' - La carta scelta è l'asso di bastoni

La versione popolare con 27 carte

La versione più popolare del gioco è quella con 27 carte (3 file da 9 carte ciascuna).
Spiegazioni dettagliate del gioco si trovano online su Base5 e Polymath, e su carta ad opera di Martin Gardner¹², Ennio Peres ³ ed altri.

Di seguito riporto la descrizione di Ennio Peres, con alcune modifiche nella parte relativa alla spiegazione dello stesso.

Presentazione

Mescolate un mazzo di 27 carte e, dopo averlo consegnato a uno spettatore, fornitegli le seguenti istruzioni:

Scegli mentalmente una di queste carte e ricorda il suo valore, senza comunicarmelo.
Tieni in mano le 27 carte, con le facce rivolte verso il basso e (procedendo da sinistra verso destra), distribuiscile una alla volta, a faccia in alto, su righe di 3 carte, fino a formare 3 colonne di 9 carte (come indicato in figura).
Dimmi in quale colonna si trova la carta da te scelta.
Raccogli in un mazzetto le 9 carte di ciascuna colonna (senza alterare l’ordine con cui le carte sono state distribuite) e ricomponi il mazzo, disponendo in un ordine a tuo piacere, i 3 mazzetti così ottenuti.
Esegui di nuovo la sequenza di istruzioni 2, 3 e 4 e poi salta al punto 6.
Esegui per la terza volta la la sequenza di istruzioni 2, 3 e 4 e poi salta al punto 7.
Distribuisci le carte sul tavolo, nel modo indicato dall’istruzione 2.

A questo punto siete in grado di indicare, senza alcuna esitazione, la carta scelta dallo spettatore.

Modalità di esecuzione

Per riuscire in tale intento, dovete osservare i seguenti accorgimenti:

Ogni volta che lo spettatore ricompone il mazzo (istruzione 4), osservate in quale posizione: superiore, centrale o inferiore (considerando il mazzo rivolto a facce in basso), colloca il mazzetto contenente la carta scelta.
Assegnate a ciascuna posizione una cifra, in base al seguente criterio: > superiore = 0, centrale = 1, inferiore = 2

(in pratica, il valore della cifra così assegnata corrisponde al numero di mazzetti che vengono messi sopra quello preso in considerazione).
Scrivete nell’ordine, da destra verso sinistra, le cifre attribuite alle tre posizioni osservate, in modo da ottenere un numero ternario; il valore di questo numero indicherà quante carte, nell’ultima configurazione ottenuta, si trovano prima della carta da indovinare (contando da sinistra verso destra e dall’alto verso il basso).
Ad esempio, se la prima volta il mazzetto viene posto nella posizione inferiore ($2$), la seconda volta nella posizione superiore ($0$) e la terza volta nella posizione centrale ($1$), scrivendo le relative cifre, da destra verso sinistra, si ottiene il numero ternario $102$.
Dato che, in decimale, questo numero corrisponde a:

$2\cdot 3^0 + 0\cdot3^1 + 1\cdot 3^2 = 2\cdot 1 + 0\cdot 3 + 1\cdot 9 = 2 + 0 + 9 = 11$

la carta da indovinare è preceduta da altre $11$ carte e, quindi è la $12\textit{ma}$

Spiegazione del trucco

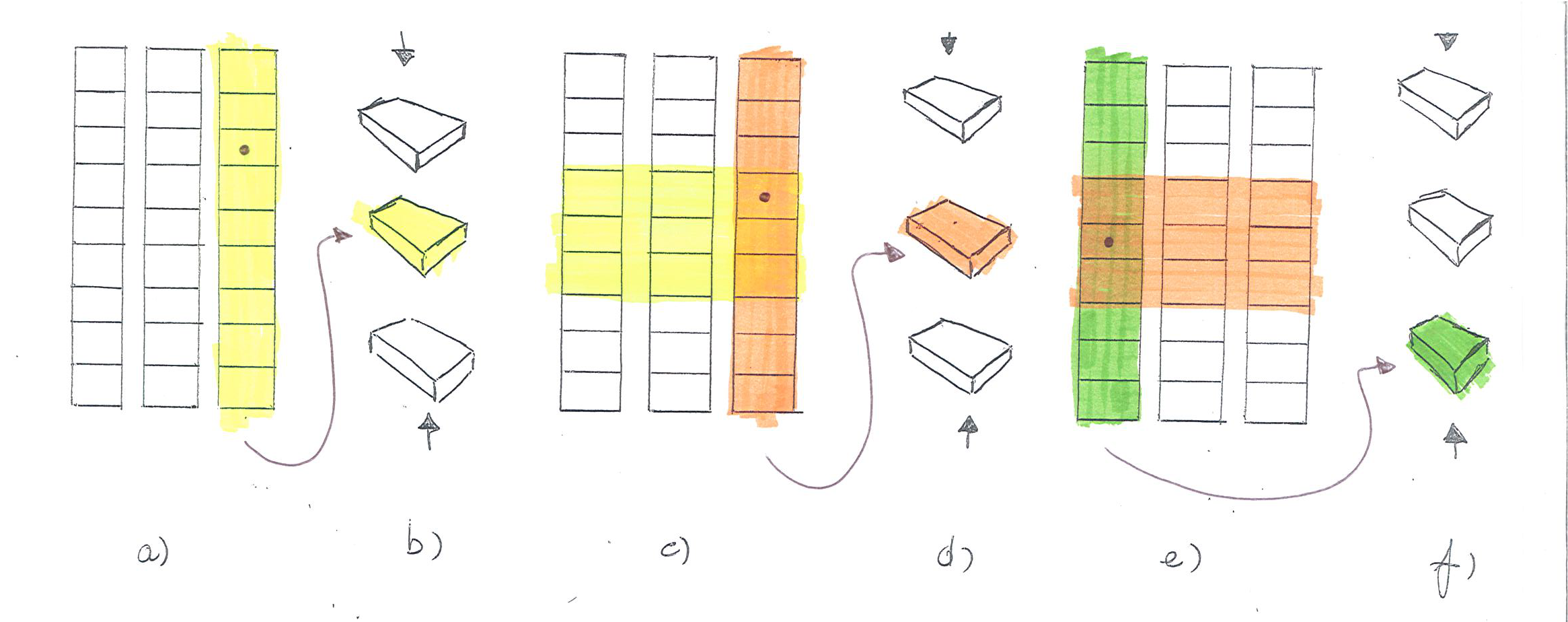
Figura 4 - Spiegazione grafica del 'Gioco delle 27 carte'

Prendiamo ad esempio il procedimento in figura e soffermiamoci sull'ultima distribuzione e successiva ricomposizione dei mazzetti (fig.4e, 4f).
Dato che la pila contenente la nostra carta viene rimessa nel mazzo in posizione $2$, ossia in coda al mazzo, ciò significa che essa sarà preceduta da due pile, ossia da $18$ carte.
Analogamente, se la pila contenente la carta da indovinare viene riposta in posizione $1$ nel mazzo (al centro), allora sarà preceduta sicuramente da $1$ pila di carte, ossia da $9$ carte.
Se invece la pila con la nostra carta viene riposta in posizione $0$ nel mazzo (in cima), allora non sarà preceduta da alcuna carta.
Quindi possiamo dire che, dopo l'ultima ricomposizione del mazzo, la pila con la nostra carta sarà preceduta da $\lbrace 0, 9, 18\rbrace $ carte a seconda che essa venga riposta rispettivamente in posizione $\lbrace 0, 1, 2\rbrace $ del mazzo.

Restiamo sempre sull'ultima ridistribuzione del mazzo (fig. 4e). Suddividiamo idealmente la pila contenente la nostra carta in $3$ gruppi:

gruppo1 (gruppo di cima): $\lbrace 1^a, 2^a, 3^a \rbrace$ carta
gruppo2 (gruppo centrale): $\lbrace 4^a, 5^a, 6^a \rbrace$ carta
gruppo3 (gruppo di coda): $\lbrace 7^a, 8^a, 9^a \rbrace$ carta

Si nota che la nostra carta si trova nel gruppo centrale, ed è quindi preceduta da $1$ gruppo ($3$ carte), all'interno della pila.
Questo perchè nella ricomposizione precedente dei mazzetti (fig. 4c), la pila contenente la nostra carta è stata riposta in posizione $1$ nel mazzo.
E' facile rendersi conto che, se nella ricomposizione precedente la pila indicata fosse stata riposta in posizione $0$ nel mazzo, allora nell'ultima ridistribuzione la carta sarebbe venuta a trovarsi nel gruppo di cima, ossia non sarebbe stata preceduta da alcuna carta, all'interno della pila. Analogamente, se nella ricomposizione precedente la pila indicata fosse stata riposta in posizione $2$ nel mazzo, allora nell'ultima ridistribuzione la carta sarebbe venuta a trovarsi nel gruppo di coda, ossia sarebbe stata preceduta da $2$ gruppi ($6$ carte), all'interno della pila.
Quindi se ne ricava che dopo l'ultima redistribuzione, il gruppo contenente la nostra carta, all'interno della pila, sarà preceduta da $\lbrace 0, 3, 6\rbrace $ carte a seconda che nella seconda ricomposizione la pila indicata sia stata riposta rispettivamente in posizione $\lbrace 0, 1, 2\rbrace $, rispettivamente.

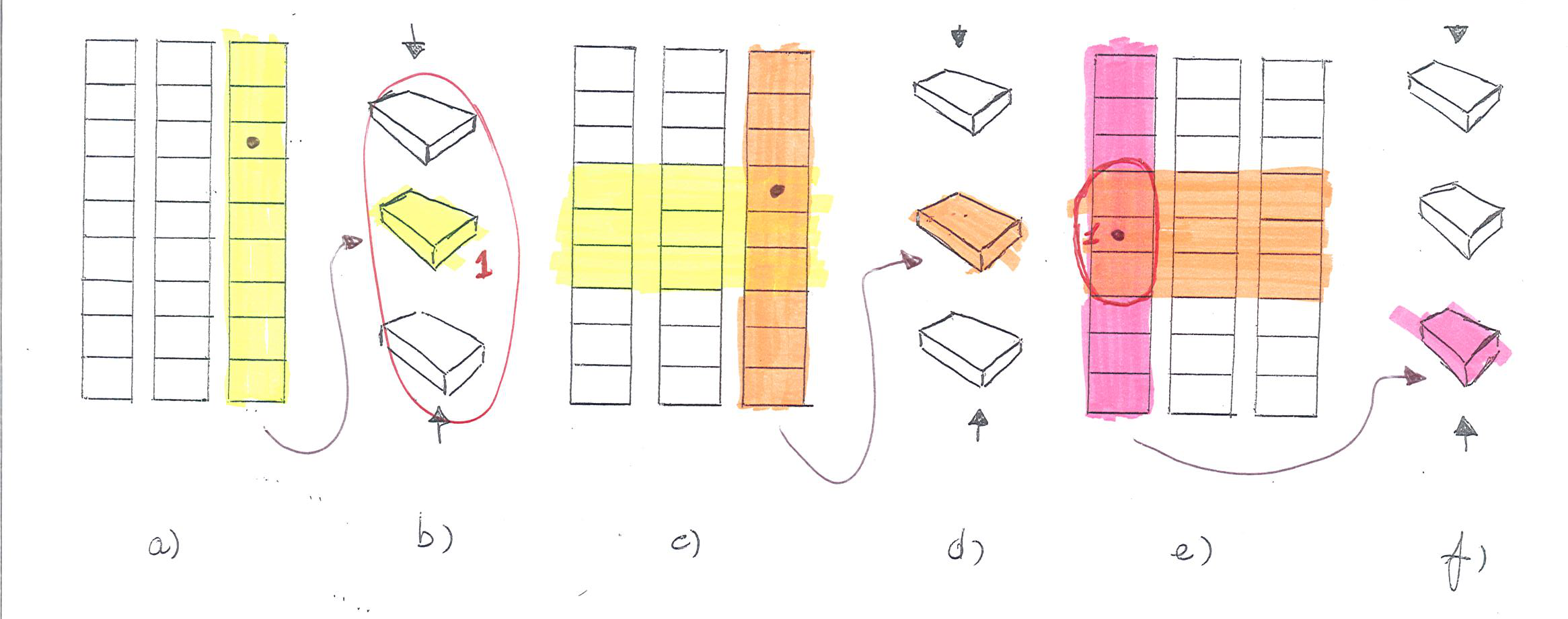
Figura 5 - Spiegazione grafica del 'Gioco delle 27 carte' - Dettaglio

Infine analizziamo la posizione che può assumere la nostra carta nel gruppo cui appartiene.
Aiutandoci graficamente con la figura 5e si può notare come nell'ultima ridistribuzione la nostra carta risulti al centro del gruppo cui appartiene, ed è quindi preceduta da $1$ carta all'interno del gruppo, se nella prima ricomposizione la pila contenente la nostra carta è stata riposta in posizione $1$ nel mazzo.
Analogamente se nella prima ricomposizione la pila contenente la nostra carta è stata riposta in posizione $0$ nel mazzo, allora nell'ultima ridistribuzione la nostra carta risulterà in cima al gruppo cui appartiene, e quindi non sarà preceduta da alcuna carta.
Se infine nella prima ricomposizione la pila contenente la nostra carta è stata riposta in posizione $2$ nel mazzo, allora nell'ultima ridistribuzione la nostra carta risulterà in coda al gruppo cui appartiene, e quindi sarà preceduta da $2$ carte.
Dunque si ha che dopo l'ultima redistribuzione, la nostra carta, all'interno del gruppo, sarà preceduta da $\lbrace 0, 1, 2\rbrace $ carte a seconda che nella prima ricomposizione la pila indicata sia stata riposta rispettivamente in posizione $\lbrace 0, 1, 2\rbrace $, rispettivamente.

A questo punto, dopo l'ultima ricomposizione del mazzo, sommando il numero di carte che precedono la carta in oggetto nel gruppo, il numero di gruppi che precedono il gruppo della nostra carta, il numero di pile che precedono la pila contenente la nostra carta, si ottiene il numero complessivo di carte che precedono la nostra carta.
Ossia posssiamo scrivere:

$n_{pre} = \lbrace 0, 1, 2\rbrace + \lbrace 0, 3, 6\rbrace + \lbrace 0, 9, 18\rbrace$

dove i valori da scegliere tra parentesi dipendono rispettivamente dalle posizioni $p_1$, $p_2$, $p_3 = \lbrace 0, 1, 2 \rbrace $ in cui viene riposta di volta in volta la pila contenente la carta.

Per cui ne possiamo ricavare la formuletta:

$n_{pre} = p_1 + 3\cdot p_2 + 9\cdot p_3$

Quindi la posizione della carta da indovinare ci sarà data da:

$n_c = p_1 + 3\cdot p_2 + 9\cdot p_3 + 1$

La variante con 32 carte (4 file da 8)

Stanco di ripetere il solito gioco con 27 carte, tempo fa trovai una variante che si prestava bene ad essere eseguita con un classico mazzo di carte napoletane.
Ossia con 4 file da 8 carte ciascuna.

Provo ad illustrarla di seguito, analogamente a quanto fatto per il gioco delle 27 carte.

Presentazione

Mescolate un mazzo di 32 carte e, dopo averlo consegnato a uno spettatore, fornitegli le seguenti istruzioni:

Scegli mentalmente una di queste carte e ricorda il suo valore, senza comunicarmelo.
Tieni in mano le 32 carte, con le facce rivolte verso il basso e (procedendo da sinistra verso destra), distribuiscile una alla volta, a faccia in alto, su righe di 4 carte, fino a formare 4 colonne di 8 carte (come indicato in figura).
Dimmi in quale colonna si trova la carta da te scelta.
Raccogli in un mazzetto le 8 carte di ciascuna colonna (senza alterare l’ordine con cui le carte sono state distribuite) e ricomponi il mazzo, disponendo in un ordine a tuo piacere, i 4 mazzetti così ottenuti.
Esegui di nuovo la sequenza di istruzioni 2, 3 e 4 e poi salta al punto 6.
Esegui per la terza volta la la sequenza di istruzioni 2, 3 e 4 e poi salta al punto 7.
Distribuisci le carte sul tavolo, nel modo indicato dall’istruzione 2.

A questo punto siete in grado di indicare, senza alcuna esitazione, la carta scelta dallo spettatore.

Modalità di esecuzione

Per riuscire in tale intento, dovete osservare i seguenti accorgimenti:

Ogni volta che lo spettatore ricompone il mazzo (istruzione 4), osservate in quale posizione: superiore, centrale superiore, centrale inferiore o inferiore (considerando il mazzo rivolto a facce in basso), colloca il mazzetto contenente la carta scelta.
Assegnate a ciascuna posizione una cifra, in base al seguente criterio: > superiore = 0, centrale superiore = 1, centrale inferiore = 2, inferiore = 3

(in pratica, il valore della cifra così assegnata corrisponde al numero di mazzetti che vengono messi sopra quello preso in considerazione).
Indicando con $p_1$, $p_2$ e $p_3$ le cifre corrispondenti alle posizioni in cui viene riposto il mazzetto scelto dopo ogni ricomposizione, si ha che dopo l'ultima ricomposizione, la carta da indovinare sarà preceduta da un numero di carte pari a:
$n_{pre} = \left\lfloor\frac{p_1}{2}\right\rfloor + p_2\cdot 2 + p_3\cdot 8$

Spiegazione del trucco

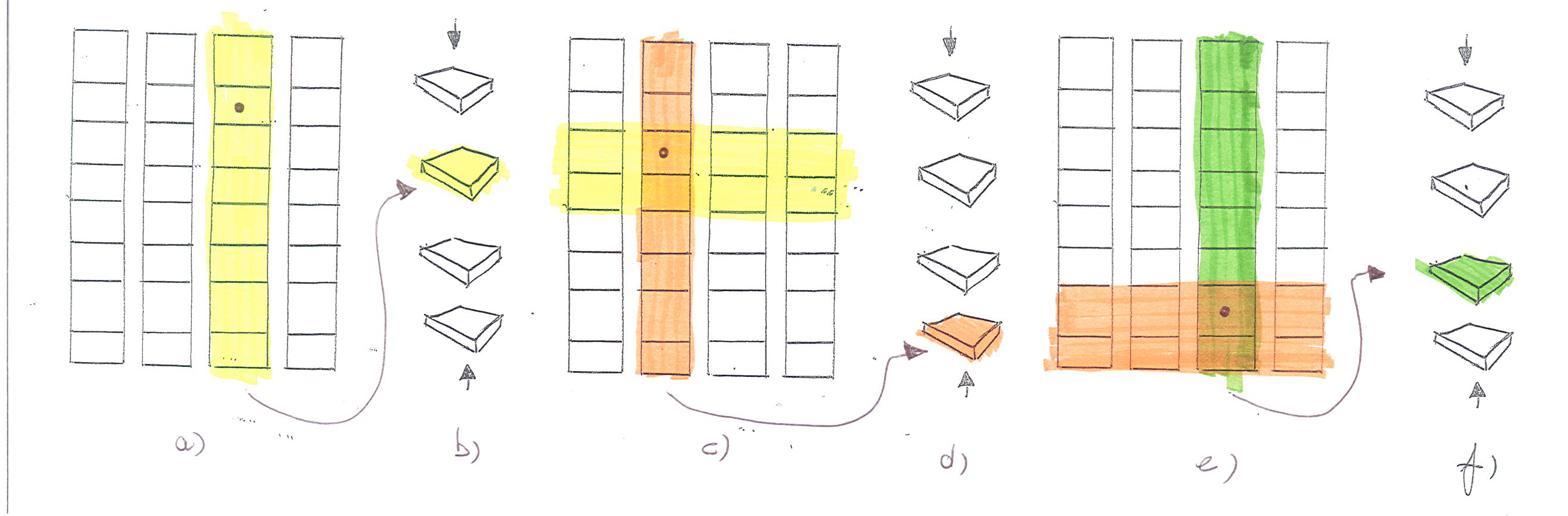
Figura 6 - Spiegazione grafica della variante a 32 carte

Prendiamo ad esempio il procedimento in figura e soffermiamoci sull'ultima distribuzione e successiva ricomposizione dei mazzetti (fig. 6e, 6f). Dato che la pila contenente la nostra carta viene rimessa nel mazzo in posizione $2$, ossia in posizione centrale inferiore, ciò significa che essa sarà preceduta da due pile, ossia da $16$ carte.
Analogamente, se la pila contenente la carta da indovinare viene riposta in posizione $1$ nel mazzo (centrale superiore), allora sarà preceduta sicuramente da $1$ pila di carte, ossia da $8$ carte.
Se invece la pila con la nostra carta viene riposta in posizione $0$ nel mazzo (in cima), allora non sarà preceduta da alcuna carta.
Se infine la pila con la nostra carta viene riposta in posizione $3$, ossia in coda al mazzo, allora sarà preceduta da $3$ pile, ossia $24$ carte.
Quindi possiamo dire che, dopo l'ultima ricomposizione del mazzo, la pila con la nostra carta sarà preceduta da $\lbrace 0, 8, 16, 24\rbrace $ carte a seconda che essa venga riposta rispettivamente in posizione $\lbrace 0, 1, 2, 3\rbrace $ del mazzo.

Restiamo sempre sull'ultima ridistribuzione del mazzo (fig. 6e). Suddividiamo idealmente la pila contenente la nostra carta in 4 gruppi:

gruppo1 (gruppo di testa): $\lbrace 1^a, 2^a \rbrace$ carta
gruppo2 (gruppo centrale superiore): $\lbrace 3^a, 4^a \rbrace$ carta
gruppo3 (gruppo centrale inferiore): $\lbrace 5^a, 6^a \rbrace$ carta
gruppo4 (gruppo di coda): $\lbrace 7^a, 8^a \rbrace$ carta

Si nota che la nostra carta si trova nel gruppo di coda, ed è quindi preceduta da $3$ gruppi ($6$ carte), all'interno della pila.
Questo perchè nella ricomposizione precedente dei mazzetti (fig. 6c), la pila contenente la nostra carta è stata riposta in posizione $3$ nel mazzo.
E' facile rendersi conto che, se nella ricomposizione precedente la pila indicata fosse stata riposta in posizione $0$ nel mazzo, allora nell'ultima ridistribuzione la carta sarebbe venuta a trovarsi nel gruppo di cima, ossia non sarebbe stata preceduta da alcuna carta, all'interno della pila. Analogamente, se nella ricomposizione precedente la pila indicata fosse stata riposta in posizione $1$ nel mazzo, allora nell'ultima ridistribuzione la carta sarebbe venuta a trovarsi nel gruppo centrale superiore, ossia sarebbe stata preceduta da $1$ gruppo ($2$ carte), all'interno della pila.
Ancora, se nella ricomposizione precedente la pila indicata fosse stata riposta in posizione $2$ nel mazzo, allora nell'ultima ridistribuzione la carta sarebbe venuta a trovarsi nel gruppo centrale inferiore, ossia sarebbe stata preceduta da $2$ gruppi ($4$ carte), all'interno della pila.
Quindi se ne ricava che dopo l'ultima redistribuzione, il gruppo contenente la nostra carta, all'interno della pila, sarà preceduto da $\lbrace 0, 2, 4, 6\rbrace $ carte a seconda che nella seconda ricomposizione la pila indicata sia stata riposta rispettivamente in posizione $\lbrace 0, 1, 2, 3\rbrace $, rispettivamente.

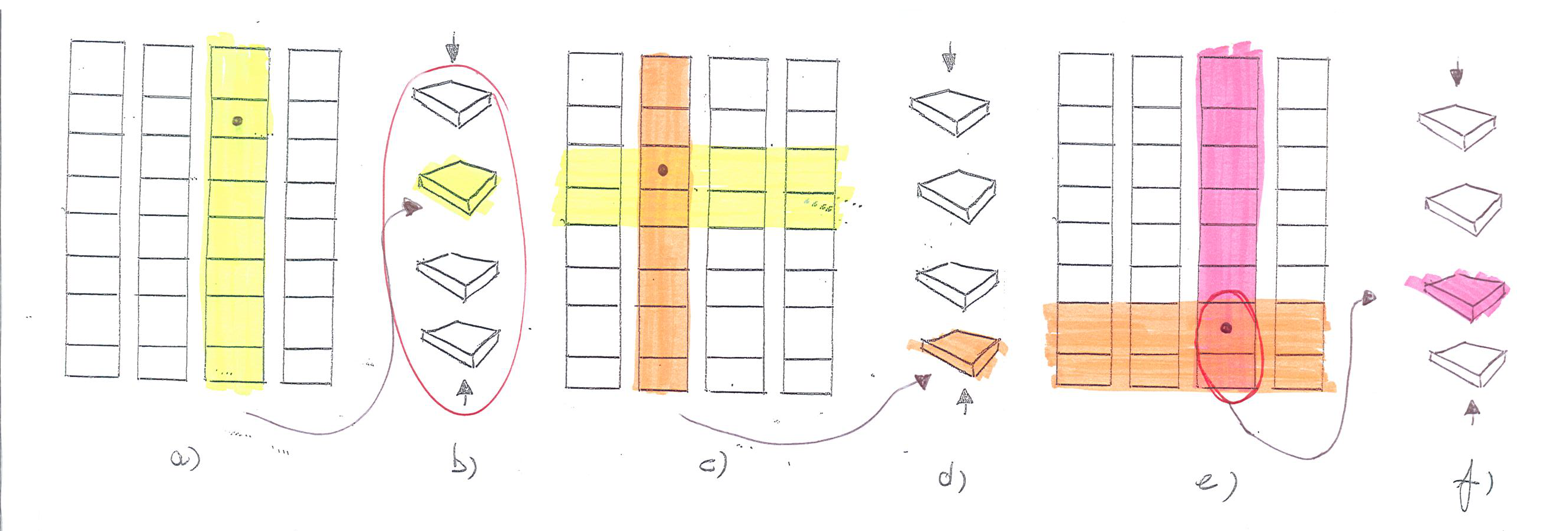
Figura 7 - Spiegazione grafica della variante a 32 carte - Dettaglio

Infine analizziamo la posizione che può assumere la nostra carta nel gruppo cui appartiene.
Aiutandoci graficamente con la figura 7e si può notare come nell'ultima ridistribuzione la nostra carta risulterà in cima al gruppo cui appartiene, e quindi non sarà preceduta da alcuna carta all'interno del gruppo, se nella prima ricomposizione la pila contenente la nostra carta è stata riposta in posizione $0$ o $1$ nel mazzo.
Analogamente se nella prima ricomposizione la pila contenente la nostra carta è stata riposta in posizione $2$ o $3$ nel mazzo, allora nell'ultima ridistribuzione la nostra carta risulterà in coda al gruppo cui appartiene, e sarà preceduta da $1$ carta.
Dunque si ha che dopo l'ultima redistribuzione, la nostra carta, all'interno del gruppo, sarà preceduta da $\lbrace 0, 1\rbrace $ carte a seconda che nella prima ricomposizione la pila indicata sia stata riposta rispettivamente in posizione $\lbrace \left[0, 1\right], \left[2, 3\right]\rbrace $, rispettivamente.

$n_{pre} = \lbrace 0, 1\rbrace + \lbrace 0, 2, 4, 6\rbrace + \lbrace 0, 8, 16, 24\rbrace$

dove i valori da scegliere tra parentesi dipendono rispettivamente dalle posizioni $p_1$, $p_2$, $p_3 = \lbrace 0, 1, 2, 3 \rbrace $ in cui viene riposta di volta in volta la pila contenente la carta, secondo le modalità spiegate sopra.

Per cui se ne ricava:

$n_{pre} = \left\lfloor\frac{p_1}{2}\right\rfloor + p_2\cdot 2 + p_3\cdot 8$

Quindi la posizione della carta da indovinare ci sarà data da:

$n_c = \left\lfloor\frac{p_1}{2}\right\rfloor + p_2\cdot 2 + p_3\cdot 8 + 1$

La generalizzazione

Incuriosito dalla trattazione ricreativa del problema presente in "Mathematical Recreations and Essays" di W.W.Ball mi son messo a cercare in rete una formula valida per il caso generale $np$ ($n$ righe e $p$ colonne).
Ebbene la generalizzazione è possibile, e viene spiegata in modo dettagliato ed esauriente nella pubblicazione "The Gergonne p-pile problem and the dynamics of the function…", di J.Harrison et al. ⁴.
Nel paper viene ricavata una formula generale che ci da la posizione della nostra carta nella pila di riferimento dopo un numero sufficiente di ridistribuzioni.
Vengono analizzati i seguenti 2 casi:

fixed column re-collection case
periodic column re-collection case

Fixed column re-collection case

Nel primo caso, ad ogni ridistribuzione delle carte, la pila scelta viene riposta sempre nella stessa posizione fissa $k$.
L'analisi di questo primo caso nell'articolo porta alla formula

$f^\ell(x) = \begin{cases} \left\lfloor r/(p-1) \right\rfloor -1 \qquad \textit{se}\;(p-1)|r\;\;\textit{e}\;\;x<\frac{r}{p-1} \\ \left\lfloor r/(p-1) \right\rfloor \end{cases}$

con $x$ che è la posizione della nostra carta nella pila scelta dopo la prima distribuzione ed è $1\le x \le n$;
con $r=kn+p-1$ dove $k$ è la posizione in cui viene riposta la pila scelta ad ogni ricomposizione ed è $0 \le k \le p-1$, $n$ è il numero di carte di una pila, e $p$ è il numero di pile (colonne);
$\ell$ è il numero di ridistribuzioni che vengono effettuate prima di indovinare la carta.
Gli autori della pubblicazione hanno dimostrato matematicamente che per $\ell > log_p {n + 1}$ la formula risulta sempre valida.
In realtà la formula può essere valida anche per valori di $\ell$ inferiori a tale limite, ma questo al momento va verificato sperimentalmente caso per caso.
Tale formula ci da proprio la posizione della carta da indovinare nella pila scelta dopo $\ell$ ridistribuzioni.

Vediamo un esempio: consideriamo il caso $9\text{x}3$ analizzato più su.
Si ha $n=9$, $p=3$, $l=3$, $\ell=3$ e consideriamo $k=1$ ad ogni ricomposizione.
La formula risulta valida dato che $\ell > log_p{(n + 1)} \Rightarrow 3 > log_3{(10)}$.
Si ha $r=kn+p-1=1\cdot 9+3-1=11$ che non è divisibile per $p-1=2$.
Pertanto la formula ci da

$f^\ell(x) = \left\lfloor \frac{r}{p-1} \right\rfloor = \left\lfloor \frac{11}{2} \right\rfloor = 5$

Ciò significa che dopo la terza ridistribuzione la carta da indovinare sarà la $5^a$ della pila scelta. Ossia, riponendo la pila scelta in posizione $1$ del mazzo dopo la terza ridistribuzione e contando dalla cima, la nostra carta sarà in posizione $9+5=14$.
Lo stesso risultato si ottiene con la formula specifica vista per il solo caso $9\text{x}3$ ossia

$n_c = 1 + 3\cdot 1 + 9\cdot 1 + 1 = 14$

Periodic column re-collection case

Nel secondo caso invece viene analizzata la situazione più generale in cui ad ogni ricomposizione la pila scelta viene riposta in una qualsiasi posizione $k_i$ con $0\le k \le p-1$.
In pratica viene utilizzata l'idea di pattern periodico, ossia viene considerato un insieme di $m$ ricomposizioni e ridistribuzioni, che viene ripetuto periodicamente.
Il pattern nello specifico ci è dato dalle $m$ posizioni $k_i$ in cui viene riposta la pila in ogni ricomposizione.
Pertanto in questo caso $\ell$ sta ad indicare la periodicità, ossia il numero di volte che viene rieseguito il pattern.
Tuttavia la formula riportata nell'articolo risulta errata (qualche errore negli indici delle sommatorie)⁵.
Ho rieffettuato il calcolo del limite che porta alla formula finale, trovando la seguente formula che sembra funzionare bene (verificata al pc)

$f^\ell(x) = \begin{cases} \left\lfloor L \right\rfloor -1 \qquad \textit{se}\;L\in\mathbb{Z}\;\;\textit{e}\;\;x < L \\ \left\lfloor L \right\rfloor \end{cases}$

dove

$L = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1$

con $1\le x \le n$; con $0 \le k \le p-1$ e con $n\ge 2$.
La formula risulta valida per $\ell > (1/m)(log_{p}{n}+1)$.
Tale formula ci da proprio la posizione della carta da indovinare nella pila scelta dopo $\ell$ riesecuzioni del pattern.
Evidentemente per i nostri scopi é necessario che la formula sia valida per $\ell = 1$.

Vediamo un esempio: consideriamo la variante $8\text{x}4$ di cui sopra.
Si ha $n=8$, $p=4$, $m=2$, $\ell=1$ e $k_1=\lbrace 0,1,2,3 \rbrace , k_2=\lbrace 0,1,2,3 \rbrace$.
Sappiamo che la formula risulta sempre valida per $\ell > (1/m)(log_{p}{n}+1) \Rightarrow \ell > (1/2)(log_{4}{8}+1) \Rightarrow \ell > 1,25$.
A noi però interessa verificare che sia valida anche per $\ell=1$.
Possiamo farlo manualmente mediante esecuzione di tutti i $16$ casi possibili, ossia tutti i casi con $n=8$, $p=4$, $m=2$, $\ell=1$ e $k_1=\lbrace 0,1,2,3 \rbrace , k_2=\lbrace 0,1,2,3 \rbrace$.
Si verifica così che la formula è valida anche per $\ell=1$.

Calcoliamo ora $L$ e valutiamo se sia intero o meno.
Si ha

$L = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1= \displaystyle\frac{2\cdot 8 + 3\cdot 8 \cdot 4}{4^2-1}+1 = \frac{112}{15}+1 = 8,4\overline{6}$

Pertanto, essendo $L$ non intero, la formula ci da

$f^\ell(x) = \left\lfloor L \right\rfloor = \left\lfloor\displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1\right\rfloor = \left\lfloor\displaystyle\frac{2\cdot 8 + 3\cdot 8 \cdot 4}{4^2-1}+1\right\rfloor = \left\lfloor \frac{112}{5}+1 \right\rfloor = 8$

Ciò significa che dopo la terza ridistribuzione la carta da indovinare sarà la $8^a$ della pila scelta. Ossia, riponendo la pila scelta in posizione $1$ del mazzo dopo la terza ridistribuzione e contando dalla cima, la nostra carta sarà in posizione $8+8=16$.
Lo stesso risultato si ottiene con la formula specifica vista per il solo caso $8\text{x}4$ ossia

$n_c = \left\lfloor \frac{2}{2}\right\rfloor + 3\cdot 2 + 1\cdot 8 + 1 = 16$

Riferimenti bibliografici

W. W. Rouse Ball, Mathematical Recreations and Essays, 12th edition, New York, 1975.
Joseph Diaz Gergonne - Wikipedia IT

M. Gardner, Enigmi e giochi matematici - Vol. V, Sansoni, Firenze, 1976. ↩
M. Gardner, I misteri della magia matematica, Sansoni, Firenze, 1985. ↩
E. Peres, L'elmo della mente, Salani, 2006. ↩
J. Harrison, T. Brennan, and S. Gapinski, The Gergonne p-pile problem and the dynamics of the function x → (x + r)/p, Discrete Applied Mathematics 82 (1998) 103–113 ↩
Ho segnalato il possibile errore al Prof. Harrison il quale mi ha gentilmente risposto, promettendomi di revisionare il paper a breve con i suoi coautori ↩

Le pile di Gergonne

Scritto da Pietro Vitelli il 07 Giugno 2017

Il gioco delle 21 carte

La versione popolare con 27 carte

Presentazione

Modalità di esecuzione

Spiegazione del trucco

La variante con 32 carte (4 file da 8)

Presentazione

Modalità di esecuzione

Spiegazione del trucco

La generalizzazione

Fixed column re-collection case

Periodic column re-collection case

Riferimenti bibliografici