... di gatti, topi, muli e altre creature

Scritto da Pietro Vitelli il 10 Novembre 2013

Molti dei problemi concernenti la matematica ricreativa, trattano di animali, persone ed oggetti di vario genere. Tra questi vanno sicuramente annoverati tutti quei quesiti in cui si chiede al lettore di contare, in vari modi e forme, le entità in gioco. Il più antico di questi problemi, nonchè primo esempio di gioco matematico giuntoci dall'antichità, è sicuramente il problema n.79 del papiro di Rhind. Il papiro di Rhind è il più esteso papiro egizio di argomento matematico giunto fino ai giorni nostri. Prende il nome da un antiquario scozzese, tale Henry Rhind, che lo acquistò nel 1858 a Luxor in Egitto. Esso risale all'incirca al 1650 a.c., periodo in cui lo scriba Ahmes lo trascrisse da un papiro precedente probabilmente composto tra il 1850 a.c. ed il 1800 a.c. ((E' lo stesso Ahmes, nell'introduzione del papiro a scrivere di averlo copiato da un papiro rislatente al tempo del faraone "Ne-ma’et-Re", che regnò tra il 1849 e il 1801 a.C.)). Attualmente è conservato presso il British Museum di Londra, con alcuni piccoli frammenti dislocati al Brooklyn Museum di New York.

Il problema 79 è forse l'unico di carattere giocoso del papiro 1; è scritto a margine dello stesso, in mezzo ad altri problemi tecnici e calcoli vari. Il testo tradotto recita così 2 :

In una proprietà ci sono 7 case, in ogni casa ci sono 7 gatti, ogni gatto acchiappa 7 topi, ogni topo mangia 7 spighe di grano, ogni spiga dà 7 hekat 3 di grano. Quante cose ci sono in tutto in questa storia?

Il problema si risolve semplicemente calcolando la somma $7+7^2+7^3+7^4+7^5$, ossia la somma dei primi $n$ termini di una serie geometrica di ragione $r$:

In realtà il primo termine della serie non va considerato, a meno che non si voglia considerare la proprietà menzionata nella storia come una delle cose da contare. Pertanto si ha:

nel nostro caso $n=5$ (le cinque cose della storia) ed $r=7$ (la quantità delle cose della storia, che si ripete); per cui il valore cercato è:

La soluzione presente nel papiro è la seguente:

Soluzione al problema n.79 presente nel papiro di Rhind

Nella parte sinistra sono elencate le quantità di ogni cosa, con in fondo la somma complessiva. Più interessante però è la parte destra della soluzione. E' ipotizzabile si tratti dell'applicazione di un metodo alternativo per il calcolo della somma dei primi $n$ termini di una serie geometrica. Mi immagino funzionasse più o meno così:

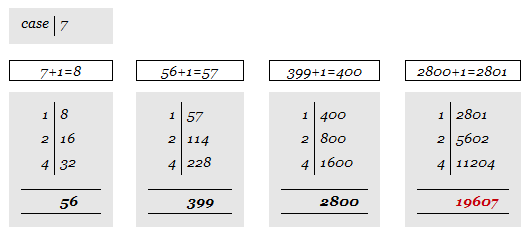
Soluzione alternativa al problema n.79 presente nel papiro di Rhind

Il metodo sfrutta 2 proprietà matematiche evidentemente note agli egiziani: 1. Ogni numero intero può essere espresso come somma di potenze di 2 ((Tale proprietà è alla base del cosiddetto "metodo del raddoppio", utilizzato dagli egiziani per eseguire le moltiplicazioni.)) 2. Raccoglimento a fattor comune. Es. $7+7^2+\cdots+7^n=7\cdot (1+7+7^2+\cdots+7^{n-1})$

Pertanto, il $7$ viene espresso come $1+2+4$, mentre il raccoglimento a fattor comune, applicato iterativamente, porta a trovare il numero cercato.

Nel corso dei secoli, fino ai giorni nostri, diverse varianti del problema sono state proposte.

Tra queste troviamo il seguente problema contenuto nella parte nona del capitolo XII del Liber Abaci di Fibonacci 4 :

N.64 - Originale N.64 - Traduzione
Septem vetule vadunt Romam Sette anziani vanno a Roma
quarum quelibet habet burdones 7, ognuno ha 7 muli,
et in quolibet burdone sunt saculi 7 ogni mulo ha 7 sacchi,
et in quolibet saculo panes 7 ogni sacco ha 7 pani,
et in quilibet panis habet cultellos 7 ogni pane 7 coltelli,
et quilibet cultellus habet vaginas 7. ogni coltello 7 fodere.
Queritur summa omnium predictorum. Si chiede la somma di tutti.

Il problema è molto simile a quello del papiro di Rhind; ci sono solo più elementi da contare. In pratica, si tratta di calcolare la somma dei primi 6 termini della serie geometrica di ragione 7 (primo termine 1 escluso)

Risultato in linea con la soluzione data nel liber abaci, che è la seguente 5 :

Moltiplica il numero delle vecchie, 7, per il numero dei muli, 7; viene 49. Moltiplica 3249 per i 7 sacchi, viene 343. Moltiplica per 7 pani; viene 2401. Moltiplica per 7 coltelli; viene 16807. Moltiplica per 7 guaine; viene 117649. Sommando tutto viene 137256.

Una successiva versione più ricreativa del rompicapo, compare in un manoscritto del 1730 circa; si tratta del ben noto enigma di St.Ives:

Enigma di St.Ives - Originale Enigma di St.Ives - Traduzione
As I was going to St. Ives, Mentre andavo a St. Ives
I met a man with seven wives, Incontrai un uomo con sette mogli.
Each wife had seven sacks, Ogni moglie aveva sette sacchi,
Each sack had seven cats, Ogni sacco aveva sette gatti,
Each cat had seven kits: Ogni gatto aveva sette mici;
Kits, cats, sacks, and wives, Mici, gatti, sacchi e mogli,
How many were there going to St. Ives? In quanti andavano a St. Ives?
Una illustrazione dell'enigma di St.Ives

Questo enigma è particolarmente interessante in quanto, nella versione originale inglese, ha la forma di una nursery rhyme; inoltre è catalogato nel database delle canzoni folk della tradizione (Roud folk song index) con numero 19772. Non ultimo, l'indovinello prevede molteplici soluzioni, tutte più o meno plausibili, che giocano sulla mancanza di informazioni circa le intezioni del gruppo incontrato. La soluzione maggiormente accettata, è quella che il solo narratore va a St.Ives; quindi $1$; questo perchè l'assunzione più comune è che il narrante incontra il gruppo di persone, animali ed oggetti, quindi questi ultimi non vanno a St.Ives bensì nella direzione opposta. Altre soluzioni sono:

  • $2802$ : il narratore incontra il gruppo, che sta procedendo più lentamente sempre verso St.Ives (in pratica li raggiunge). In questo caso quindi tutti vanno a St.Ives; ossia $1+1+7+7^2+7^3+7^4=2802$.
  • $2800$ : come sopra, ma senza i 2 uomini. Questo perchè nel penultimo rigo si parla di mici, gatti, sacchi e mogli senza menzionare gli uomini.
  • $2$ : ossia solo i 2 uomini. Questo perchè il testo non è chiaro e quindi è plausibile anche che le donne non fossero presenti.
  • $0$ : è una variante della prima risposta (quella "standard", $1$); in questo caso si assume che il narratore non includa anche a se stesso, nelle entità da contare.
  • $2753$ : il verbo andare, fa pensare che si dabbano contare solo le persone e gli animali (i sacchi da soli non vanno da nessuna parte!). Quindi $1+1+7+7^3+7^4=2753$
  • $2751$ : come sopra, ma senza i 2 uomini. Questo perché nel penultimo rigo si parla solo di mici, gatti, sacchi e mogli.
  • $9$ : si considerano solo le persone coinvolte nel racconto, gli animali vengono esclusi in quanto si trovano nei sacchi, che "non vanno" ma "vengono trasportati".
  • $7$: come sopra, ma senza i 2 uomini.
  • Minimo $1$ : con certezza possiamo solo dire che 1 persona sta andando a St.Ives: il narratore.
L'uomo che andava a Camogli

Infine, una versione analoga, tutta italiana dell'enigma è stata proposta nel 1908 6 :

Per una strada che mena a Camogli passava un uomo con sette mogli. E ogni moglie aveva sette sacche, e ogni sacca aveva sette gatte, e ogni gatta sette gattini. Fra gatti e gatte e sacchi e mogli, in quanti andavano, dite, a Camogli?

Si tratta di una traduzione e adattamento dell'enigma di St.Ives, pertanto le soluzione sono le stesse viste sopra.

Riferimenti bibliografici

  1. C.B.Boyer a proposito del contenuto del papiro dice: "Molti dei calcoli contenuti nel Papiro di Rhind erano evidentemente esercizi pratici per giovani studenti. Sebbene gran parte di essi sia di natura pratica, in alcuni casi sembra che lo scriba avesse in mente indovinelli o giochetti matematici" ↩

  2. La traduzione più completa del papiro è quella di A.B.Chase, un appassionato di Egittologia americano. ↩

  3. l'hekat era una unità di mura di capacità dell'antico Egitto, utilizzata per misurare il grano. Corrisponde a 4,8 litri circa. ↩

  4. Il Liber abaci è un manoscritto medievale in latino di argomento matematico, scritto nel 1202 da Leonardo Pisano detto "Fibonacci"; il capitolo XII contiene per intero problemi di matematica ricreativa. ↩

  5. Università di Firenze - Convegno - Il liber abaci. pag.32. ↩

  6. L'uomo che andava a Camogli. Camilla del Soldato, Enciclopedia dei ragazzi. 1908. ↩

comments powered by Disqus